
РАЗДЕЛЫ
ГЛАВНАЯ
СТАТЬИ
СКАЧАТЬ
О DARK BASIC
ПОЛЕЗНЫЕ ССЫЛКИ
CODE DEMOS
Посетители
ПРИМЕЧАНИЕ!
Сайт рекомендуется просматривать в браузере Opera.
ОСВЕЩЕНИЕ.
6. Модель освещения.
Освещенность произвольно взятой точки P, появившуюся из-за источника света, излучающего во все стороны (omnilight) в общем случае будем вычислять по уравнению Фонга:
ambient = Ka,
diffuse = Kd * cos(N, L),
specular = Ks * pow(cos(R, V), Ns),
intensity = ambient + amp * (diffuse + specular).
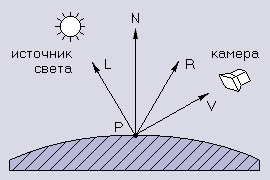
Здесь использованы следующие обозначения:
Ka коэффициент фоновой интенсивности (характеристика окружающей среды)
Kd коэффициент рассеяния (характеристика поверхности)
Ks коэффициент отражения (характеристика поверхности)
Ns коэффициент вида отражения (характеристика поверхности)
amp "мощность" источника света
P рассматриваемая точка
N нормаль к поверхности изображаемого объекта в точке P
L вектор, проведенный из точки P в источника света (луч света)
V вектор, проведенный из точки P в "точку зрения" камеры
R отраженный луч света (отражение L относительно N)
ambient "фоновая" освещенность
diffuse "рассеянная" освещенность
specular "отраженная" освещенность
intensity освещенность (суммарная)
cos(A,B) косинус угла между векторами A и B
Это уравнение даже поддается относительно простому объяснению - освещенность как бы складывается из фонового уровня освещенности, рассеянного (по всем направлениям - а значит, и по направлению глаза) в этой точке света от источника и отраженного (тоже в глаз) света от источника.
Как обычно, расчеты по этой формуле дадут довольно реалистичный результат, но считать все это для каждой точки грани слишком медленно.
Да, косинус угла между векторами считается как
cos(A,B) = A*B/(|A|*|B|),
где A*B - скалярное произведение векторов, |A| и |B| - их длины. Поэтому имеет смысл все векторы перед использованием привести к длине 1, тогда косинус угла между векторами будет равен их скалярному произведению. Небольшая оптимизация.
(Автором данной статьи является Андрей Аксенов. Адрес в FIDO: 2:5036/5.47)
E-mail автора сайта (webmaster)